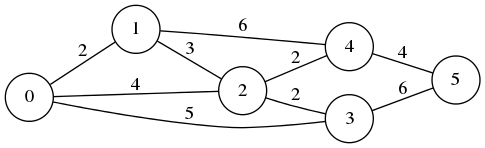
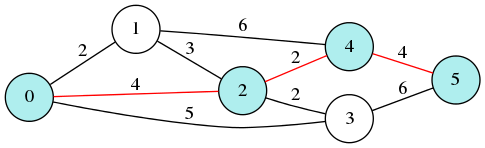
昨日のダイクストラ法を C でやってみた。
#include
#include
#include
#define N 6
typedef struct edge {
int dest;
int cost;
} Edge;
typedef struct node {
Edge *edges[N];
int edge_num;
bool done;
int cost;
int from;
} Node;
void MakeEdge(Node *nodes[], int a, int b, int cost);
void PrintRoute(Node *nodes[], int start, int goal);
void FreeNodes(Node *nodes[]);
int main(void)
{
Node *nodes[N];
Node *start_node, *n, *n2;
Node *done_node;
Edge *e;
int i, j;
int start, goal;
// initialize graph.
for (i = 0; i < N; i++) {
nodes[i] = (Node *)malloc(sizeof(Node));
nodes[i]->done = false;
nodes[i]->cost = -1;
nodes[i]->from = -1;
nodes[i]->edge_num = 0;
for (j = 0; j < N; j++) {
nodes[i]->edges[j] = NULL;
}
}
MakeEdge(nodes, 0, 1, 2);
MakeEdge(nodes, 0, 2, 4);
MakeEdge(nodes, 0, 3, 5);
MakeEdge(nodes, 1, 2, 3);
MakeEdge(nodes, 2, 3, 2);
MakeEdge(nodes, 1, 4, 6);
MakeEdge(nodes, 2, 4, 2);
MakeEdge(nodes, 4, 5, 4);
MakeEdge(nodes, 3, 5, 6);
start = 0;
goal = 5;
start_node = nodes[start];
start_node->cost = 0;
start_node->done = true;
for (i = 0; i < start_node->edge_num; i++) {
e = start_node->edges[i];
n = nodes[e->dest];
n->cost = e->cost;
n->from = start;
}
while (true) {
done_node = NULL;
for (i = 0; i < N; i++) {
n = nodes[i];
if (n->done || n->cost < 0) {
continue;
} else {
for (j = 0; j < nodes[i]->edge_num; j++) {
e = n->edges[j];
n2 = nodes[e->dest];
if (n2->cost < 0) {
n2->cost = nodes[i]->cost + e->cost;
n2->from = i;
} else if (n->cost + e->cost < n2->cost) {
n2->cost = n->cost + e->cost;
n2->from = i;
}
}
if (done_node == NULL || n->cost < done_node->cost) {
done_node = n;
}
}
done_node->done = true;
}
if (done_node == NULL) {
break;
}
}
printf("%d\n", nodes[goal]->cost);
PrintRoute(nodes, start, goal);
FreeNodes(nodes);
return 0;
}
void MakeEdge(Node *nodes[], int a, int b, int cost)
{
Edge *e1, *e2;
e1 = (Edge *)malloc(sizeof(Edge));
e1->dest = b;
e1->cost = cost;
nodes[a]->edges[nodes[a]->edge_num] = e1;
nodes[a]->edge_num++;
e2 = (Edge *)malloc(sizeof(Edge));
e2->dest = a;
e2->cost = cost;
nodes[b]->edges[nodes[b]->edge_num] = e2;
nodes[b]->edge_num++;
return;
}
void PrintRoute(Node *nodes[], int start, int goal)
{
int route[N];
int hop = 0;
route[hop] = goal;
for (hop = 0; route[hop] != start; hop++) {
route[hop + 1] = nodes[route[hop]]->from;
}
printf("%d", route[hop--]);
for (; hop >= 0; hop--) {
printf(" -> %d", route[hop]);
}
printf("\n");
return;
}
void FreeNodes(Node *nodes[])
{
int i, j;
for (i = 0; i < N; i++) {
for (j = 0; j < nodes[i]->edge_num; j++) {
free(nodes[i]->edges[j]);
}
free(nodes[i]);
}
return;
}
takatoh@nightschool $ ./dijkstra 10 0 -> 2 -> 4 -> 5