月: 2016年6月

一様分布する乱数から、正規分布に従う乱数を生成する方法に、Box-Muller法というのがある。
Wikipediaによれば、(0,1) 区間の一様分布乱数2つ（X,Y）から、下の式で2つの正規分布乱数 $ Z_1 $ と $ Z_2 $ が得られる。

$$
Z_1=\sqrt{-2log{X}}\cos{2\pi{Y}}
Z_2=\sqrt{-2log{X}}\sin{2\pi{Y}}
$$

$ Z_1 $ と $ Z_2 $ は標準正規分布となるので、これらに標準偏差 σ をかけて平均 μ を足してやれば、任意の正規分布に従う乱数が得られる。

Ruby で 10000個の乱数を発生させるスクリプトを書いてみた。ここでは平均 μ=1.0、標準偏差 σ=0.2 とした。

# encoding: Windows-31J

class BoxMuller
  def initialize(mu, sigma)
    @mu = mu
    @sigma = sigma
    @r = Random.new
    @z2 = nil
  end

  def rand
    if @z2
      z1 = @z2
      @z2 = nil
    else
      x = @r.rand
      y = @r.rand
      z1 = Math.sqrt(-2.0 * Math.log(x)) * Math.sin(2 * Math::PI * y)
      @z2 = Math.sqrt(-2.0 * Math.log(x)) * Math.cos(2 * Math::PI * y)
    end
    @sigma * z1 + @mu
  end
end

bm = BoxMuller.new(1.0, 0.2)
10000.times do |i|
  puts bm.rand
end

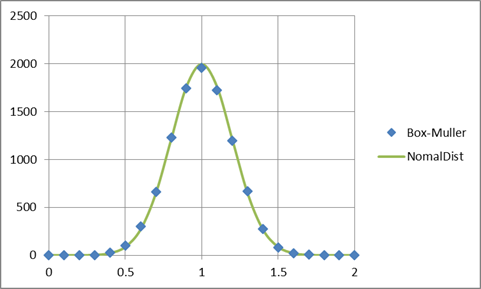
結果を Excel でグラフ化してみた。水色の点が 0.1 単位のヒストグラム。黄緑の線が Excel に用意されている NORM.DIST 関数で描いたもの（スケールを合わせるために NORM.DIST 関数の値は 1000 倍している）。

こうしてみると、ほぼぴったりと正規分布になっているようだ。

ちなみに Excel で平均値と標準偏差を求めたら、それぞれ μ=0.997、σ=0.201 となった。