takatoh's blog – Learning programming languages.
モンテカルロ法で円周率を求めるプログラムを C で書いてみたんだけど、その中で使っている sqrt() 関数が「定義されていない参照」だと言われてコンパイルできない。
takatoh@nightschool $ gcc -Wall -lm -o pi pi.c /tmp/ccfG4PRE.o: 関数 `main' 内: pi.c:(.text+0x81): `sqrt' に対する定義されていない参照です collect2: error: ld returned 1 exit status
Windows の（Strawberry Perl についてた）gcc ではちゃんとコンパイルできたのに。なんで？
昨日のダイクストラ法を C でやってみた。
#include
#include
#include
#define N 6
typedef struct edge {
int dest;
int cost;
} Edge;
typedef struct node {
Edge *edges[N];
int edge_num;
bool done;
int cost;
int from;
} Node;
void MakeEdge(Node *nodes[], int a, int b, int cost);
void PrintRoute(Node *nodes[], int start, int goal);
void FreeNodes(Node *nodes[]);
int main(void)
{
Node *nodes[N];
Node *start_node, *n, *n2;
Node *done_node;
Edge *e;
int i, j;
int start, goal;
// initialize graph.
for (i = 0; i < N; i++) {
nodes[i] = (Node *)malloc(sizeof(Node));
nodes[i]->done = false;
nodes[i]->cost = -1;
nodes[i]->from = -1;
nodes[i]->edge_num = 0;
for (j = 0; j < N; j++) {
nodes[i]->edges[j] = NULL;
}
}
MakeEdge(nodes, 0, 1, 2);
MakeEdge(nodes, 0, 2, 4);
MakeEdge(nodes, 0, 3, 5);
MakeEdge(nodes, 1, 2, 3);
MakeEdge(nodes, 2, 3, 2);
MakeEdge(nodes, 1, 4, 6);
MakeEdge(nodes, 2, 4, 2);
MakeEdge(nodes, 4, 5, 4);
MakeEdge(nodes, 3, 5, 6);
start = 0;
goal = 5;
start_node = nodes[start];
start_node->cost = 0;
start_node->done = true;
for (i = 0; i < start_node->edge_num; i++) {
e = start_node->edges[i];
n = nodes[e->dest];
n->cost = e->cost;
n->from = start;
}
while (true) {
done_node = NULL;
for (i = 0; i < N; i++) {
n = nodes[i];
if (n->done || n->cost < 0) {
continue;
} else {
for (j = 0; j < nodes[i]->edge_num; j++) {
e = n->edges[j];
n2 = nodes[e->dest];
if (n2->cost < 0) {
n2->cost = nodes[i]->cost + e->cost;
n2->from = i;
} else if (n->cost + e->cost < n2->cost) {
n2->cost = n->cost + e->cost;
n2->from = i;
}
}
if (done_node == NULL || n->cost < done_node->cost) {
done_node = n;
}
}
done_node->done = true;
}
if (done_node == NULL) {
break;
}
}
printf("%d\n", nodes[goal]->cost);
PrintRoute(nodes, start, goal);
FreeNodes(nodes);
return 0;
}
void MakeEdge(Node *nodes[], int a, int b, int cost)
{
Edge *e1, *e2;
e1 = (Edge *)malloc(sizeof(Edge));
e1->dest = b;
e1->cost = cost;
nodes[a]->edges[nodes[a]->edge_num] = e1;
nodes[a]->edge_num++;
e2 = (Edge *)malloc(sizeof(Edge));
e2->dest = a;
e2->cost = cost;
nodes[b]->edges[nodes[b]->edge_num] = e2;
nodes[b]->edge_num++;
return;
}
void PrintRoute(Node *nodes[], int start, int goal)
{
int route[N];
int hop = 0;
route[hop] = goal;
for (hop = 0; route[hop] != start; hop++) {
route[hop + 1] = nodes[route[hop]]->from;
}
printf("%d", route[hop--]);
for (; hop >= 0; hop--) {
printf(" -> %d", route[hop]);
}
printf("\n");
return;
}
void FreeNodes(Node *nodes[])
{
int i, j;
for (i = 0; i < N; i++) {
for (j = 0; j < nodes[i]->edge_num; j++) {
free(nodes[i]->edges[j]);
}
free(nodes[i]);
}
return;
}
takatoh@nightschool $ ./dijkstra 10 0 -> 2 -> 4 -> 5
ダイクストラ法とは、グラフ上の最短経路問題をとくアルゴリズム。↓このページに詳しいアルゴリズムの説明がある。
cf. ダイクストラ法（最短経路問題） – deq notes
Ruby でやってみた。
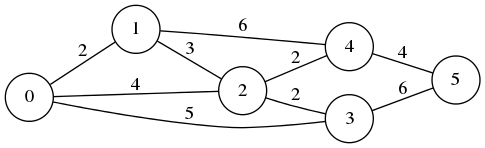
例題は、上のページにもあるこのグラフ（ただしノードにつけた番号のせいか上下が逆になっている）。
円（ノード）に番号がふられ、ノードをつなぐ辺（エッジ）にはそこを通るときのコスト（距離とも時間とも解釈できる）が付されている。この中の任意の 2 つのノードをつなぐ最短経路とコストを求めるのが最短経路問題だ。
今回は 0 番のノードをスタートし 5 番のノードをゴールとする最短経路とそのコストを求めてみる。
#!/usr/bin/env ruby
# encoding: utf-8
class Node
attr_reader :name
attr_accessor :done, :cost, :from
def initialize(name)
@name = name
@edges = []
@done = false
@cost = nil
@from = nil
end
def add_edge(edge)
@edges << edge
end
def each_edge
@edges.each{|e| yield(e) }
end
end
Edge = Struct.new(:dest, :cost)
def make_edge(nodes, a, b, cost)
nodes[a].add_edge(Edge.new(b, cost))
nodes[b].add_edge(Edge.new(a, cost))
end
nodes = []
0.upto(5) do |i|
nodes << Node.new(i)
end
edges = [
[0, 1, 2], # [node_a, node_b, cost]
[0, 2, 4],
[0, 3, 5],
[1, 2, 3],
[2, 3, 2],
[1, 4, 6],
[2, 4, 2],
[4, 5, 4],
[3, 5, 6]
]
edges.each do |a, b, cost|
make_edge(nodes, a, b, cost)
end
start = 0
goal = 5
start_node = nodes[start]
start_node.cost = 0
start_node.done = true
start_node.each_edge do |edge|
n = nodes[edge.dest]
n.cost = edge.cost
n.from = start_node.name
end
while true do
done_node = nil
nodes.each do |node|
if node.done || node.cost.nil?
next
else
node.each_edge do |e|
n = nodes[e.dest]
if n.cost.nil?
n.cost = node.cost + e.cost
n.from = node.name
else
if node.cost + e.cost < n.cost
n.cost = node.cost + e.cost
n.from = node.name
end
end
end
if done_node.nil? || node.cost < done_node.cost
done_node = node
end
end
end
done_node.done = true
break if nodes.all?{|n| n.done }
end
puts nodes[goal].cost
route = [goal]
begin
node = nodes[route.first]
route.unshift(node.from)
end
until route.first == start
puts route.map(&:to_s).join(" -> ")
実行結果：
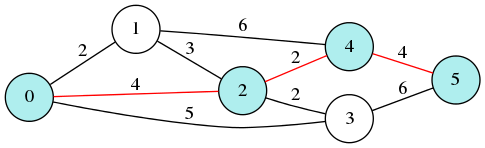
takatoh@nightschool $ ruby dijkstra.rb 10 0 -> 2 -> 4 -> 5
というわけで、最短経路は 0 -> 2 -> 4 -> 5、コストは 10 という答えが得られた。これは上のリンク先の答えと同じなので、あっていると思っていいだろう。
昨日のプログラムに、サブディレクトリのファイルを再帰的にリストアップする -r オプションをつけてみた。
#include
#include
#include
#include
#include
#include
void listfiles(char *path, int recursive);
void joinpath(char *path, const char *path1, const char *path2);
int main(int argc, char **argv)
{
char path[256];
char result;
int recursive = 0;
while ((result = getopt(argc, argv, "r")) != -1) {
switch(result) {
case 'r':
recursive = 1;
break;
case '?':
exit(1);
}
}
if (argc == optind) {
strcpy(path, ".");
} else {
strcpy(path, argv[optind]);
}
listfiles(path, recursive);
return 0;
}
void listfiles(char *path, int recursive)
{
DIR *dir;
struct dirent *dp;
struct stat fi;
char path2[256];
dir = opendir(path);
for (dp = readdir(dir); dp != NULL; dp = readdir(dir)) {
if (dp->d_name[0] != '.') {
joinpath(path2, path, dp->d_name);
stat(path2, &fi);
if (S_ISDIR(fi.st_mode)) {
if (recursive) {
listfiles(path2, recursive);
}
} else {
printf("%s\n", path2);
}
}
}
closedir(dir);
return;
}
void joinpath(char *path, const char *path1, const char *path2)
{
strcpy(path, path1);
strcat(path, "/");
strcat(path, path2);
return;
}
takatoh@nightschool $ ./listfiles -r . ./stack/linkedlist.c ./stack/linkedlist.h ./stack/main.c ./listfiles ./fib.c ./btreesort.c ./linkedlist.c ./web_color_code.c ./strrand.c ./bmp/win-jpeg.bmp ./bmp/dog2.bmp ./bmp/bmp.c ./bmp/win-4.bmp ./bmp/win-16-1.bmp ./bmp/dog.bmp ./bmp/win-32-bf-888.bmp ./bmp/win-8.bmp ./bmp/win-32.bmp ./bmp/win-16-bf-324.bmp ./bmp/win-32-t.bmp ./bmp/win-16-t.bmp ./bmp/bmp.h ./bmp/os-4.bmp ./bmp/os-1.bmp ./bmp/win-32-bf-td.bmp ./bmp/win-1.bmp ./bmp/win-png.bmp ./bmp/win-8-td.bmp ./bmp/os-8.bmp ./bmp/os-24.bmp ./bmp/win-4-rle.bmp ./bmp/win-16.bmp ./bmp/win-32-bf-833.bmp ./bmp/Makefile ./bmp/win-24.bmp ./bmp/pic1.bmp ./bmp/win-8-rle.bmp ./bmp/bmpinfo.c ./code2rgb.c ./btree/btree.c ./btree/btree.h ./btree/main.c ./mergesort.c ./quicksort.c ./transhex.c ./heapsort.c ./filter.c ./greeting.c ./bubblesort.c ./listfiles.c
readdir() 関数を使う。ファイルとディレクトリの判別には stat() 関数の戻り値（stat 構造体）の st_mode を使う。これにはディレクトリかどうかを判別する S_ISDIR マクロが用意されている。今回はディレクトリでなければファイルだと思うことにした。
あと、「.」で始まるファイル（とディレクトリ）は無視した。
#include <stdio.h>
#include <dirent.h>
#include <sys stat.h="">
#include <string.h></string.h></sys></dirent.h></stdio.h>
void listfiles(char *path);
void joinpath(char *path, const char *path1, const char *path2);
int main(int argc, char **argv)
{
char path[256];
if (argc == 1) {
strcpy(path, ".");
} else {
strcpy(path, argv[1]);
}
listfiles(path);
return 0;
}
void listfiles(char *path)
{
DIR *dir;
struct dirent *dp;
struct stat fi;
char path2[256];
dir = opendir(path);
for (dp = readdir(dir); dp != NULL; dp = readdir(dir)) {
if (dp->d_name[0] != '.') {
joinpath(path2, path, dp->d_name);
stat(path2, &fi);
if (!S_ISDIR(fi.st_mode)) {
printf("%s\n", path2);
}
}
}
closedir(dir);
return;
}
void joinpath(char *path, const char *path1, const char *path2)
{
strcpy(path, path1);
strcat(path, "/");
strcat(path, path2);
return;
}
実行例：
takatoh@nightschool $ ./listfiles ./listfiles ./fib.c ./btreesort.c ./linkedlist.c ./web_color_code.c ./strrand.c ./code2rgb.c ./mergesort.c ./quicksort.c ./listfiles_r.c ./transhex.c ./heapsort.c ./filter.c ./greeting.c ./bubblesort.c ./listfiles.c
takatoh@nightschool $ ./listfiles btree btree/btree.c btree/btree.h btree/main.c
名前は Potov。「ポトフ」と発音してほしい。
cf. https://github.com/takatoh/Potov
Explorer-like とはつまり、左側にディレクトリツリーが、右側に選択したディレクトリの中の画像（サムネイル）が表示されるってこと。ディレクトリツリーの表示には jsTree を、画像の表示には Colorbox を使っている。表示専用で、画像の移動なんかは出来ない（するつもりもない）。
メインの実装言語は Ruby。フレームワークには Sinatra を使っている。一応シングルページアプリケーション。
画像を追加したり移動したりはファイルシステムで物理的に行う。今のところ、サムネイルを手動で作成する必要があるので、このへんは今後改修したいところだ。