日: 2017年3月21日

ちょっと面白いものを見つけた。

cf. LEDドームのLEDの並びを決めるのに使用した計算式 – jakaladaのブログ

球面上に任意個の点を一様分布させる、座標を求めるもの。一般化螺旋集合（generalized spiral set）というものを使っている。元の資料（論文）はここ。

cf. 多数の点を球面上に一様分布させるソフトウェアGSS Generator

上のリンク先のブログでは Python を使っているので、Ruby でやってみた。

#!/usr/bin/env ruby
# encoding: utf-8

require 'gss'
require 'optparse'
require 'csv'

options = {}
opts = OptionParser.new
opts.banner = "Generate points with uniform distribution on the sphere."
opts.on("-c", "--cartesian", "Cartesian coordinate."){|v|
  options[:cartesian] = true
}
opts.on_tail("-h", "--help", "Show this message."){|v|
  print opts.help
  exit
}
opts.on_tail("-v", "--version", "Show version."){|v|
  puts "v#{GSS::VERSION}"
  exit
}
opts.parse!

r = ARGV.shift.to_f
n = ARGV.shift.to_i

gss = GSS::GSS.new
points = gss.generate(r, n)
points.each do |p|
  if options[:cartesian]
    coord = p.to_cartesian
    print coord.to_csv
  else
    print [p.r, p.theta, p.phi].to_csv
  end
end

# encoding: utf-8

require "gss/polar_point"

module GSS
  class GSS
    def generate(r, n)
      theta_1 = Math::PI
      phi_1 = 0.0

      points = []
      points << PolarPoint.new(r, theta_1, phi_1)
      2.upto(n) do |k|
        h_k = -1.0 + 2.0 * (k - 1) / (n - 1)
        theta_k = Math.acos(h_k)
        phi_k = points.last.phi + 3.6 / Math.sqrt(n) * 1 / Math.sqrt(1 - h_k ** 2)
        phi_k = phi_k.infinite? ? 0.0 : phi_k % (Math::PI * 2.0)
        points << PolarPoint.new(r, theta_k, phi_k)
      end
      points
    end
  end # of class GSS
end # of module GSS

# encoding: utf-8
module GSS
  class PolarPoint
    attr_reader :r, :theta, :phi

    def initialize(r, theta, phi)
      @r = r
      @theta = theta
      @phi = phi
    end

    def to_cartesian
      x = @r * Math.sin(@theta) * Math.cos(@phi)
      y = @r * Math.sin(@theta) * Math.sin(@phi)
      z = @r * Math.cos(@theta)
      [x, y, z]
    end
  end # of class PolarPoint
end # of module GSS

最初のがコマンドで、あとの2つがライブラリ。引数に球の半径と配置したい点の個数を指定すると、各点の極座標を CSV 形式で出力する。

^o^ > ruby -Ilib exe/gss_gen 1.0 600

極座標じゃなく、デカルト座標（XYZ座標）がほしい時には --cartesian オプション。

^o^ > ruby -Ilib exe/gss_gen --cartesian 1.0 600

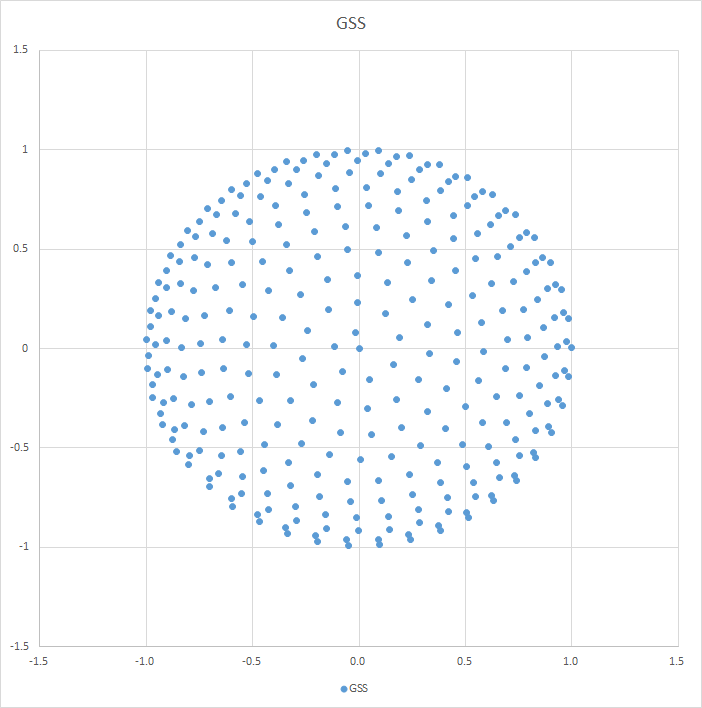
下の図は、発生させた600個の点のうち下半分の300個を XY 平面上に投影した図。

各点を順に線でつないでみると、螺旋になっているのがよくわかる。

……なんか螺旋が逆になってるな。元論文じゃ球面を下から見たと書いてあるからそのせいか？

ともあれ、それらしいのはできた。ただし、最初と最後の点の座標を調整するのはやってない。時間があったらやってみよう。