日: 2016年7月23日

逆関数法で指数分布する乱数を生成する

[0,1)区間の一様乱数から、指数分布にならう乱数を生成するには、逆関数法というのが使える。
指数分布の密度関数は、パラメータをτとすると：
$$ f(\tau)=\lambda e^{-\lambda\tau} $$
であり、分布関数 g(τ) は：
$$ g(\tau)=\int^\tau_{-\infty}{\lambda e^{-\lambda\tau}}d\tau=1-e^{-\lambda\tau} $$
となる。g(τ)は 0～1 の値をとるので、この逆関数：
$$ \tau=-\frac{1}{\lambda}log(1-g(\tau)) $$
の g(τ) の代わりに一様乱数を入力してやれば、τ は指数分布する乱数になる。

じゃあ Ruby でやってみよう。

# encoding: Windows-31J

class RandExpon
  def initialize(lamda)
    @lamda = lamda
    @r = Random.new
  end

  def rand
    -1.0 / @lamda * Math.log(1 - @r.rand)
  end
end

expon = RandExpon.new(0.5)
  10000.times do |i|
  puts expon.rand
end
expon

λ=0.5とし、10000個の乱数を発生させている。
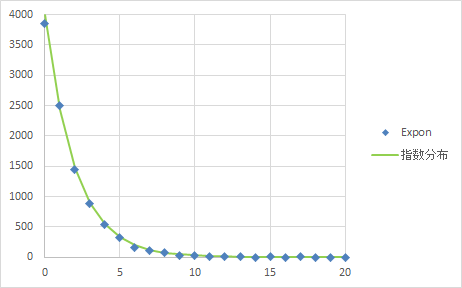
これを Excel でグラフ化したのがこれ。

「指数分布」の曲線は、上に書いた密度関数の曲線を、スケールを合わせるために8000倍して描いている。乱数はちゃんと指数分布になっているようだ。

参考にしたページ：
　cf. http://www.ishikawa-lab.com/montecarlo/4shou.html